PlantUML to compute diagrams!

This post is the Part 2 of my fun project on comparing execution times of different languages using the Queen Problem. [Link to Queen Problem Solution and Analysis—Part 1]

Once again, let me first show you some results …

Solution to the 5-Queen problem
*[NOTE: Solution to the 8-Queen problem, which is the canonical version of the N-Queen problem, draws chessboards too small for a teaser. It will appear later in this post, so keep reading. ]*

… and then take you through the journey.

Content Waypoints

Motivation and Flashback
Solution Explanation
Results
Prior Art

Motivation and Flashback

In October 2021, I presented PlantUML at Smart Coffee Break, an internal tech talk series at work. While preparing for my talk, I explored PlantUML in depth and discovered its preprocessor. Initially, I was skeptical about its usefulness compared to writing the diagram descriptions directly.

However, a few days later, I realized that the preprocessor could function as a general purpose programming language! This insight inspired me to include some examples of computing diagrams, rather than “just” drawing them, to make my tech talk more entertaining. Thus began my journey of learning the PlantUML preprocessor with fun examples. The Prior Art section showcases some of my creations using the preprocessor as a programming language.

When working on the Queen problem performance analysis recently, I thought it would be cool to draw all those solutions. This was a fine reason to resume my work with the PlantUML preprocessor.

Solution Explanation

In the first step, I decided to translate my C++ recursive solution (described in Part 1) to PlantUML. The only change needed would be to replace printing the solution with drawing the solution. However, this is not so simple, I had to use a few hacks to get it working, which I will describe below.

EXPOSITION

Now, you may say it is more efficient to compute the solutions with C++, then draw them with PlantUML, and you would be right! In a professional environment, I would follow that approach too. However, I use the PlantUML preprocessor for computation for two reasons:

To demonstrate the capability of the PlantUML preprocessor as a full-fledged Turing complete language—a graphical language, if you will.

Solving the problem in another language and only drawing the solution with PlantUML is mundane and boring. This is a fun project and I want to have fun.

Hack to use an array

Preprocessor does not provide an array or hashmap data structure, but the Queen problem solution requires a few arrays. To resolve this, I hacked string concatenation to simulate an array. This hack creates a variable for each array element by concatenating the array name with the index. For example, if we need an array named pawns with index positions 0 to 7, we would create 8 variables, pawns0, pawns1, …, pawns7.

For convenience and readability, I defined a few helper functions for this hack:

!function $to_variable($array_name, $index)
'This helper function "hacks" an array.
    !return %string($array_name + $index)
!endfunction

!function $get($array_name, $index)
'This helper function gets the value of an array element.
    !return %get_variable_value($to_variable($array_name, $index))
!endfunction

!procedure $set($array_name, $index, $value)
'This helper function sets the value of an array element.
    %set_variable_value($to_variable($array_name, $index), $value)
!endprocedure

Hack to draw a chessboard

To draw a chessboard, I needed a way to draw a two-dimensional grid. I had previously used Salt wireframe diagrams to draw grids, so I started from there. I ran into a problem with the table syntax, which The-Lum addressed in this answer to my question on the PlantUML forum. Their answer helped me fix the syntax, although my eventual solution did not require Salt.

The below code draws the two-dimensional grid, with the key points being:

Draw a vertical bar (|) for each column.
Close a row with a vertical bar (|) and add a newline.

!function $make_chessboard()
    !$diagram = ""
    !$row = 0
    'The below two while loops "hack" a table to draw a chessboard.
    !while $row < $n
        !$column = 0
        !while $column < $n
            !$diagram = $diagram + "| "
            !$column = $column + 1
        !endwhile
        !$diagram = $diagram + " |" + %newline()
        !$row = $row + 1
    !endwhile
    !return $diagram
!endfunction

With the grid layout ready, placing the Queens solution was easy. While drawing the grid, the Unicode character for Queen (♛) is placed at the squares denoted by the row and column numbers in the solution. All other squares are left blank.

Here is the code snippet for placing the Queens:

' snip ... '
!$row = 0
!while $row < $n
    !$column = 0
    !while $column < $n
        ' snip ... '
        !if $get("placed_queen_id", $row) == $column
            !$diagram = $diagram + "♛"
        !endif
        !$column = $column + 1
    !endwhile
    ' snip ... '
    !$row = $row + 1
!endwhile

Hack to colour the chessboard in alternating colours

For the chessboard to look realistic, we need to colour it in alternating light and dark colours. I chose lichess’s default chessboard colours. Since lichess is open source , it was easy to obtain the RGB values here.

There are several ways to achieve the alternating colouring. I felt the even-odd approach was the simplest. The preprocessor does not have a modulo division function, hence I used the below integer division hack. [However, this hack may soon be unnecessary if my upcoming pull request to PlantUML gets approved. ]

!function $is_odd($number)
'"hack" to check if a number is odd.
'Perform integer division by 2, then multiply by 2. Due to truncation, the value will
'not be equal to the starting number if it is odd.
    !return ($number / 2 * 2) != $number
!endfunction

SIDENOTE

I later remembered I had the same problem during my exploration in 2021. Back then, I had used a more primitive approach.

!function $is_even($num)
    !$num_str = %string($num)
    !$last_digit = %substr($num_str, %strlen($num_str) -1, 1)
    !return ($last_digit == "0"\
            || $last_digit == "2"\
            || $last_digit == "4"\
            || $last_digit == "6"\
            || $last_digit == "8")
!endfunction

Hack to arrange the solutions

The last piece of the puzzle is arranging the multiple solutions in an aesthetically pleasing manner. For this, I used my final hack: make each solution a class in a class diagram! The class name is the solution number while the chessboard showing the solution is a class field.

!procedure $draw_solution()
    class **$solution_counter** {
        $make_chessboard()
    }
    !$solution_counter = $solution_counter + 1
!endprocedure

Results

Below are the solutions, starting with the canonical 8-Queens problem, followed by the others in numerical order.

TIP

Some drawings below are too large to view easily on the webpage. You can open them in a new tab/window or download them for better clarity. The images are in SVG format, allowing you to zoom in for a clearer view.

Solution to the 8-Queens problem

Solution to the 1-Queens problem

Solution to the 2-Queens problem

Solution to the 3-Queens problem

Solution to the 4-Queens problem

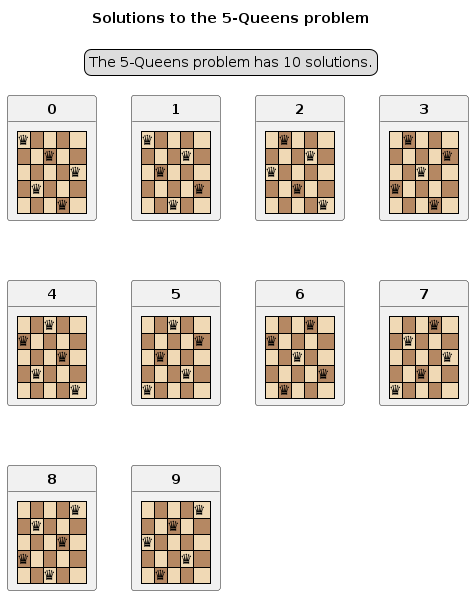
Solution to the 5-Queens problem

Solution to the 6-Queens problem

Solution to the 7-Queens problem

Solution to the 9-Queens problem

Solution to the 10-Queens problem

Solution to the 11-Queens problem

Prior Art

Here are some fun and educational examples from my previous exploration in 2021.

Test cricket matches hosting data in a hierarchical structure

Data about Test cricket matches hosted at various grounds is available in JSON format. This data is drawn in a hierarchical structure based on the ground’s location (city, country), while also recursively computing the sum of all lower levels.

Hierarchical structure representing Test matches hosting data
*[For more clarity, please open image in new tab and zoom in.]*

Collatz sequence for a range of numbers

The preprocessor draws separate diagrams showing the Collatz sequence for a range of numbers. The diagrams for two arbitrarily chosen numbers, 18 and 65, are shown below as examples. The complete set of diagrams for numbers 1 to 100 is available in my github repository here.

More examples

The complete list of examples and more explanation is available in my document Fun and learning with the PlantUML preprocessor.
An overview and demo of PlantUML features is available at PlantUML demo … and other useful stuff. Example source codes are also available in the github repository.